이번 포스팅에서는 Segment Tree(세그먼트 트리)의 개념과 Python Code를 설명합니다. Code만 참고하실 분은 포스팅 가장 아랫부분으로 내려가시면 됩니다.
Segment Tree(세그먼트 트리, 구간트리) 알고리즘
세그먼트 트리는 배열에서 구간 사이의 합을 구하거나 i번째 값을 바꾸는 문제에서 주로 이용됩니다.
아래와 같은 상황을 생각해 보겠습니다. ( 배열A가 주어짐 )
- 1) 구간 l,r ( l ≤ r )을 주고 l ~ r 사이 배열의 합( A[l] + A[l+1] + ... + A[r-1] + A[r] 값을 구하라
- 2) 배열 A에서 i번째 값을 v로 바꾸기. ( A[i] = v
위 연산을 for문 만을 이용해 푼다면 합을 구하는데 O(N)이, M회 연산을 수행하면 O(NM) 시간복잡도를 가집니다.
구간합을 S[i]를 미리 구해둔다고 생각해 볼 수도 있습니다.
- S[i] = A[1] + A[2] + ... + A[i] 입니다.
- 구간 i ~ j 사이의 합은 S[j] - S[i-1] 입니다.
하지만 구간합 S[i]를 이용할 때 배열 A값을 바꾸는 2번 연산을 수행하려면 모든 S를 변경해야 하므로 O(N)의 시간복잡도를 가집니다.
이런 상황에서 Segment Tree는 O(lgN) 시간복잡도로 위 문제를 해결할 수 있습니다.
먼저, Segment Tree의 모습을 보면 아래와 같은 모습을 가집니다.

위 그림은 N=10인 세그먼트 트리의 모습입니다. 가장 아래에 있는 리프노드는 배열의 수 그 자체를 가리키고, 다른 노드들은 왼쪽 자식과 오른쪽 자식의 합을 저장합니다.
1) 리프 노드 : 배열의 수 그자체
2) 다른 노드 : 왼쪽 자식과 오른쪽 자식의 합을 저장
따라서 어떤 노드의 번호가 i라면 해당 노드의 왼쪽 자식은 2*i, 오른쪽 자식은 2*i+1입니다.
위 노드 번호를 Tree에 표기하면 아래와 같은 모습을 가집니다.

- 위 그림에서 만약 N이 2의 제곱꼴 일 경우를 Full Binary Tree라고 하며, 리프노드 N개를 가지고 lg(N)의 높이(H)를 가집니다. 또 필요한 노드의 개수는 2*N - 1개입니다.
- 만약 N이 2의 제곱꼴이 아니라면 높이 H = [ lg(N) ] 이며 총 필요 노드의 개수는 2*(H+1) - 1개입니다.
구현
이제 세그먼트 트리의 성질을 알아봤으니 어떻게 구현하는지 알아보도록 하겠습니다. Python으로 세그먼트 트리를 구현할 때는 최초 Init 함수를 통해 Tree 구조를 만들어야합니다. 이후 문제 초반에 설명한 구간 사이의 합을 구하는 함수와 배열의 값을 업데이트하는 함수를 구현하도록 하겠습니다.
초기화 ( init 함수 )
def init(node, start, end):
# node가 leaf 노드인 경우 배열의 원소 값을 반환합니다.
# node가 리프 노드인 경우, 리프 노드는 배열의 그 원소를 가져야 하기 때문에 tree[node] = a[start]가 됩니다.
if start == end :
tree[node] = l[start]
return tree[node]
else :
# 재귀함수 호출을 통해 왼쪽 자식과 오른쪽 자식 합을 저장합니다.
tree[node] = init(node*2, start, (start+end)//2) + init(node*2+1, (start+end)//2+1, end)
return tree[node]Init 함수의 node 인자로는 최초 root node인 1을, start = 0, end=n-1 값을 인자로 넘겨줍니다.
node가 leaf node가 아닐 경우 ( start ≠ end ) tree[node] 값으로 왼쪽 자식과 오른쪽 자식의 합을 호출하여 저장합니다.
node의 왼쪽 자식은 node*2이며, 담당하는 구간은 start 부터 ( start + end ) // 2까지입니다.
node의 오른쪽 자식은 node*2+1이며, 담당하는 구간은 ( start + end ) // 2 + 1부터 end 까지입니다.
이를 위해 재귀함수를 이용할 수 있습니다.
합 찾기( subSum 함수 )
포스팅 초반에 언급한 구간 l ~ r 사이의 합을 찾는 문제를 다시 생각해 봅시다. 구간 left, right가 주어졌을 때 Segment Tree를 이용해 합을 찾으려면 left, right가 포함된 노드의 값만 찾아 합해주면 됩니다.
예를 들어 left = 0, right = 9 라면 루트 노드 하나로 전체 합을 알 수 있습니다.

left = 2, right = 4 인 경우는 아래와 같습니다.
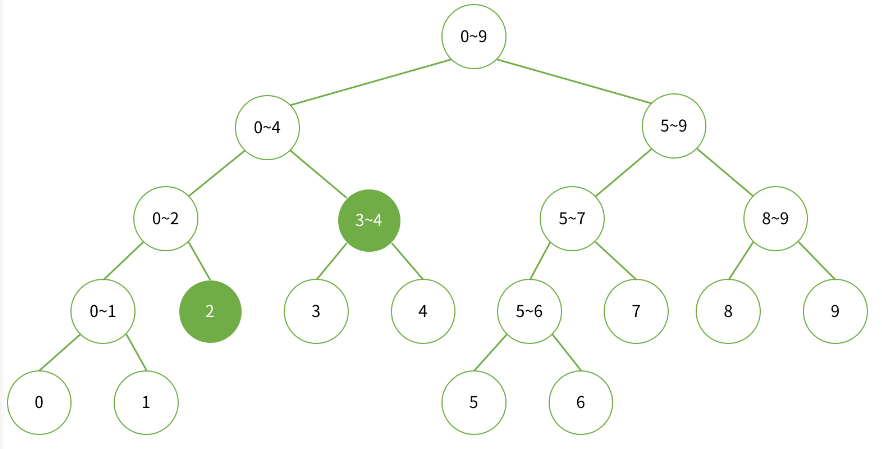
left = 5, right = 8 인 경우는 아래와 같습니다.
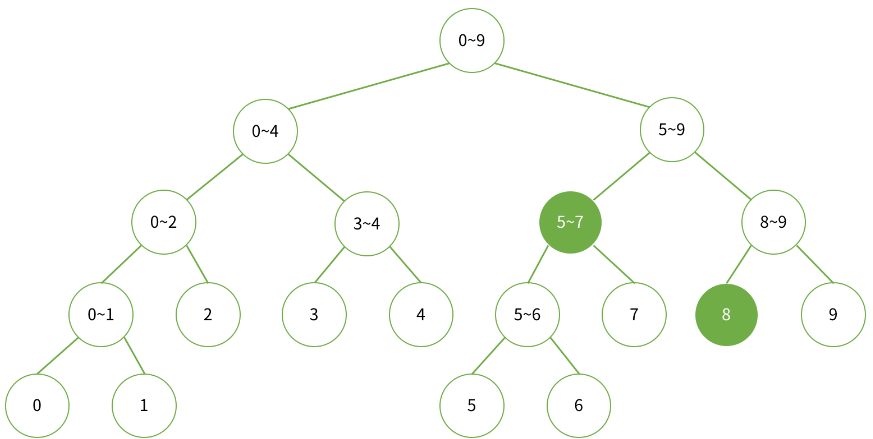
left = 3, right = 9 인 경우는 아래와 같습니다.

예시들을 보면 이해가 가시나요? Segment Tree의 각 노드 들은 특정한 구간의 합을 담당하고 있습니다. 때문에 root node부터 탐색하면서 자식 노드가 내가 원하는 구간을 담당하는 노드인지 확인하고, 더 이상 자식을 탐색할 필요가 없을 때까지 탐색해 나가야 합니다.
여기서 각 node가 담당하고 있는 구간을 [start, end], 합을 구하고자하는 구간을 [left, right]라 한다면 탐색 시에 다음과 같은 4가지 경우가 있습니다.
1. [ left, right ] 와 [ start, end ] 가 겹치지 않는 경우. ( 더 이상 탐색 X )
2. [ left, right ] 가 [ start, end ] 를 완전히 포함하는 경우. ( 더 이상 탐색 X )
3. [ left, right ] 가 [ start, end ] 에 완전히 포함되는 경우.
4. [ left, right ] 와 [ start, end ] 가 걸쳐져 있는 경우 ( 1, 2, 3 제외 나머지 경우 )
1번의 경우, 현재 탐색 중인 노드의 구간이 찾고자 하는 구간과 전혀 겹치지 않으므로 0을 반환하고 탐색을 종료합니다.
2번의 경우, 현재 탐색중인 노드의 구간이 찾고자하는 구간에 모두 들어와 있으므로 해당 노드의 값을 반환하고 탐색을 종료합니다.
3번, 4번의 경우, 현재 탐색중인 노드의 구간이 찾고자 하는 구간에 정확히 도달하지 않았으므로 왼쪽 자식노드와 오른쪽 자식 노드를 재탐색 합니다.
# node가 담당하는 구간 [start, end]
# 합을 구하고자 하는 구간 [left, right]
def subSum(node, start, end, left, right) :
# 1번 경우) 노드가 담당하는 구간과 찾고자하는 구간이 겹치지 않음. 더 이상 탐색을 이어갈 필요가 없다.
if left > end or right < start :
return 0
# 2번 경우) [start, end]는 구하고자하는 [left, right] 사이에 포함됨. 자식 node의 값을 모두 대표하고 있기때문에 더이상 호출하지 않아도 된다.
if left <= start and end <= right :
return tree[node]
# 3, 4번 경우) 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색을 시작해야한다.
# node 의 왼쪽 자식은 node*2, 오른쪽 자식은 node*2+1이 됩니다.
# node가 담당하는 구간이 [start,end] 라면 왼쪽 자식은 [start,(start+end)/2], 오른쪽 자식은 [(start+end)/2+1,end]를 담당
return subSum(node*2, start, (start+end)//2, left, right) + subSum(node*2 + 1, (start+end)//2+1, end, left, right)init 함수와 마찬가지로 node, start, end를 인자로 활용하지만 찾고자하는 구간을 나타내는 left, right 값도 함께 전달합니다. 앞서 말한 1번 경우일 경우 0 값을 반환하고, 2번 경우는 tree[node] 값을 반환합니다. 3,4번 경우에는 자식노드를 구간과 함께 재귀 호출하여 구합니다.
수 변경( Update 함수 )
합을 구했다면, 중간에 배열의 값이 변하는 경우 수를 Update 하는 방법도 알아보겠습니다.
배열의 수를 업데이트했다면 당연히 segment Tree의 노드 값도 변경해 줘야 합니다.
예를 들어 배열의 3번째 값을 업데이트한 경우는 아래와 같이 Segment Tree 노드값의 변화가 있습니다.
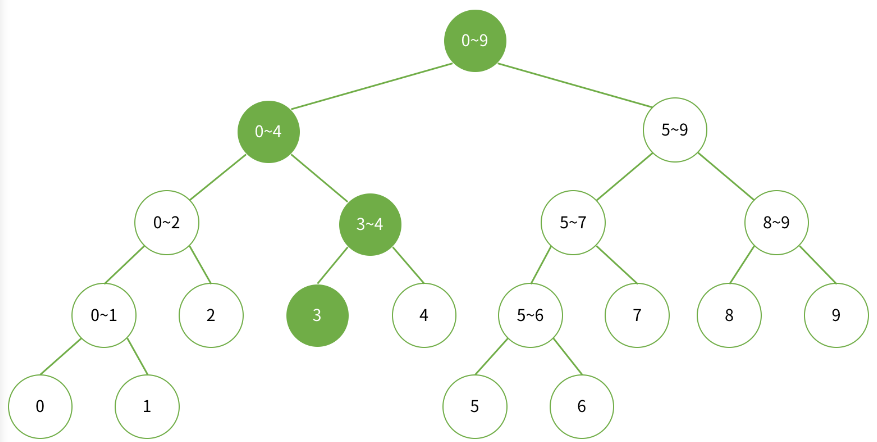
배열의 5번 값을 변경한 경우입니다.

두 예시를 보면 배열에서 변경한 값을 root node에서부터 자식 노드를 탐색하며 node의 담당 구간이 변경 된 index를 포함하는 경우에만 값을 업데이트 해주는 방식입니다.
배열 A에서 i번째 수를 val 이라는 값으로 변경한다면, 기존에 가진 값과 val 값의 차이인 diff 값을 구해야 합니다.
diff = val - A[i] 로 구할 수 있으며, index가 담당 구간에 포함되는 지 확인하여 업데이트 합니다.( 2가지 경우 )
1. [ start, end ] 에 i가 포함되는 경우.
2. [ start, end ] 에 i 가 포함되니 않는 경우.
node 의 담당 구간인 start, end에 인덱스 i가 포함되는 경우에는 diff 만큼 값을 변경합니다.
만약 node의 담당 구간에 인덱스 i가 포함되지 않으면 탐색을 종료합니다.
def update(node, start, end, index, diff) :
if index < start or index > end :
return
tree[node] += diff
# 리프 노드가 나올때까지 계속 탐색
if start != end :
update(node*2, start, (start+end)//2, index, diff)
update(node*2+1, (start+end)//2+1, end, index, diff)
위에서 살펴본 내용을 바탕으로 백준 2042번 구간 합 구하기 문제를 풀 수 있습니다. 전체 코드를 조합하면 아래와 같은 코드가 됩니다.
예제 1) 백준 2042번 코드
import sys
from math import log2, ceil
input = sys.stdin.readline
def init(node, start, end):
# node가 leaf 노드인 경우 배열의 원소 값을 반환합니다.
# node가 리프 노드인 경우, 리프 노드는 배열의 그 원소를 가져야 하기 때문에 tree[node] = a[start]가 됩니다.
if start == end :
tree[node] = l[start]
return tree[node]
else :
# 재귀함수 호출을 통해 왼쪽 자식과 오른쪽 자식 합을 저장합니다.
tree[node] = init(node*2, start, (start+end)//2) + init(node*2+1, (start+end)//2+1, end)
return tree[node]
# node가 담당하는 구간 [start, end]
# 합을 구하고자 하는 구간 [left, right]
def subSum(node, start, end, left, right) :
# 1번 경우) 노드가 담당하는 구간과 찾고자하는 구간이 겹치지 않음. 더 이상 탐색을 이어갈 필요가 없다.
if left > end or right < start :
return 0
# 2번 경우) [start, end]는 구하고자하는 [left, right] 사이에 포함됨. 자식 node의 값을 모두 대표하고 있기때문에 더이상 호출하지 않아도 된다.
if left <= start and end <= right :
return tree[node]
# 3, 4번 경우) 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색을 시작해야한다.
# node 의 왼쪽 자식은 node*2, 오른쪽 자식은 node*2+1이 됩니다.
# node가 담당하는 구간이 [start,end] 라면 왼쪽 자식은 [start,(start+end)/2], 오른쪽 자식은 [(start+end)/2+1,end]를 담당
return subSum(node*2, start, (start+end)//2, left, right) + subSum(node*2 + 1, (start+end)//2+1, end, left, right)
def update(node, start, end, index, diff) :
if index < start or index > end :
return
tree[node] += diff
# 리프 노드가 나올때까지 계속 탐색
if start != end :
update(node*2, start, (start+end)//2, index, diff)
update(node*2+1, (start+end)//2+1, end, index, diff)
n, m, k = map(int, input().rstrip().split())
l = []
h = int(ceil(log2(16)))
tSize = 1 << ( h+ 1)
tree = [0] * tSize
for _ in range(n) :
l.append(int(input().rstrip()))
init(1, 0, n-1)
for _ in range(m+k) :
a, b, c = map(int, input().rstrip().split())
if a == 1 :
b = b-1
diff = c - l[b]
l[b] = c
update(1, 0, n-1, b, diff)
elif a == 2 :
print(subSum(1, 0, n-1 ,b-1, c-1))'개발공부 > Python알고리즘' 카테고리의 다른 글
| [Python] 이분탐색 bisect 라이브러리 사용법 코드 (0) | 2023.06.06 |
|---|---|
| [Python] 바이너리 인덱스 트리(BIT, 펜윅 트리) 구현 (1) | 2023.06.04 |
| [Python]dictionary를 이용한 알고리즘 시간 단축(feat. hashtable) (0) | 2023.02.04 |
| [Python] Flask vs FastAPI vs gRPC 비교와 예제 (0) | 2023.01.29 |
| [알고리즘] 다익스트라 vs 크루스칼/프림 차이를 알아보자 (0) | 2023.01.17 |
댓글